All of the world’s major central banks have been practicing “politics of cheap money” in recent years and have therefore set their base rates close to zero. This “glut of money” has pushed share prices higher and has hurt savers who have had to put up with negative real interest rates in recent years.
However, the upturn in the economy will be accompanied by a rise in interest rates, which analysts currently expect. We are already seeing the first signs of it in the USA: the FED will reduce its bond purchase program – up to now, the FED has bought back monthly securities worth 85 billion US dollars. In January, this number is expected to drop by as much as 10 billion US dollars.
Although a rapid return to “normal” base rates in the euro area is currently unlikely, we want to present such a scenario and assess its implications.
An often used benchmark is the current yield on 10-year German government bonds (federal bonds). There is also a financial instrument that is directly linked to this yield: the federal government bond liability (FGBL).
In this article, we describe the reaction of the FGBL to changes in interest rates and yields of German government bonds. We have already presented a way for small investors to benefit from interest rate changes on German government bonds here.
For those in a hurry: There is a negative correlation between the interest rate level and the FGBL. An increase in yields on German government bonds of 1 percentage point causes the FGBL to fall between 7 and 8 %, depending on the current price. In order to invest in the FGBL, retail investors can use so-called ETFs. These (e.g. from Comdirect) can be bought through a broker. We recommend using low-cost online brokers such as Captrader or OnVista. You can find more attractive broker offers with the help of our comparison calculator.
What is the federal government bond liability (FGBL)?
The FGBL is a futures contract on a fictitious government bond of the federal republic of Germany with a 10-year duration and a coupon of 6 % p.a.
The FGBL behaves like a fixed-interest bond – rising interest rates or interest rate levels mean falling prices. You can find out more about base rates and bond prices here.
The subject of the contract are federal bonds with a remaining duration (at the time of delivery) of no less than 8.5 years and no more than 10.5 years. In addition, the bonds must originate from an issue with a volume of no less than 5 billion Euros.
This future is traded on the Eurex stock exchanges. There are always 3 futures available. The contracts expire at the end of March, June, September and December – i.e. at the end of each quarter.
Currently (January 2, 2014 – 10:41), the FGBL for March 2014 stands at 138.86 Euros. Applied to an existing bond, this means that you pay around 140 euros to receive 6 euros a year in interest over the next 10 years. In the 10th year, the bond is redeemed and you get back the nominal amount (100 euros). This results in an effective interest rate of approx. 1.73% per year.
How is the price of the FGBL calculated?
With a given interest rate level, it is easy to calculate the theoretical value (“fair value”) of a bond. And since the FGBL is nothing more than a fictitious bond, we can also do this calculation for the FGBL.
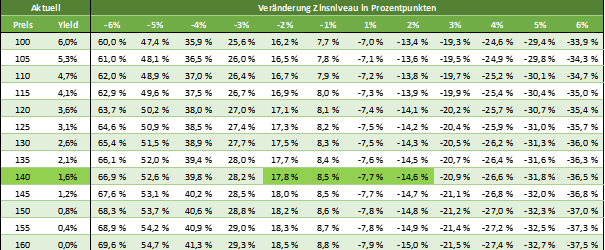
Assuming an interest rate level of 2.0%, the future should stand at around 136 (135.93) points. This is calculated by discounting the 10 interest payments and the redemption payment to the present value. 136 points thus represent the present value of the future interest and redemption payments.
This connection can be explained even more simply graphically. Each point on the following line corresponds to a change in the interest rate level of 10 basis points, i.e. 0.1 %.
How can the yield of the FGBL be calculated?
Of course, you can also reverse this consideration: What interest rate level does a FGBL level of 130 points imply?
From a mathematical point of view, this calculation is a little more difficult. This is the effective interest rate, i.e. the interest rate with which we must discount all future interest and redemption payments in order to achieve a cash value of 0 Euros. In this case, we get a polynomial of the 10th degree and there is no formula for it, only approximation methods.
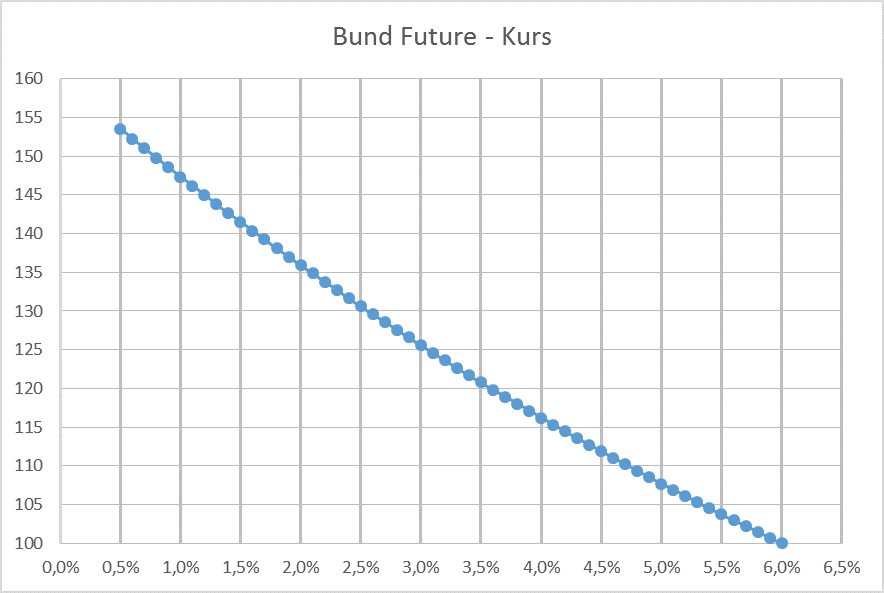
However, we are relieved of this heavy mathematical work by Excel or the function Rendite (). Thus, the effective yield of a 10-year bond with a price of 130 points is 2.56 %.
This connection is also easier to understand graphically. Each point along the line corresponds to a change in the FGBL of 1 point.
The theoretical maximum price of the FGBL is often set at 160 Euros. Of course, the price can also rise above this value, but this would imply a negative interest rate. This is not impossible per se, but economically rather unlikely or unreasonable.
How does the FGBL change in the case of a change in interest rates?
Of course, it is interesting to know how the FGBL changes if the yield on German government bonds rises by 1 percentage point.
As you may have guessed, this cannot generally be said for every level of the FGBL. This is because the first derivation of the FGBL after the price (first chart) is not constant. The chart is almost linear, but not entirely. Therefore, the derivation is different at every point (at every level of the FGBL) and therefore is also the overall change.
But of course, this connection can be visualized with the following table.
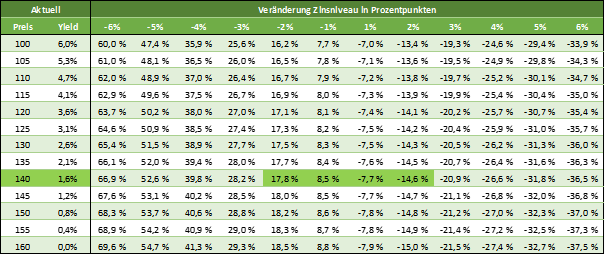
The left column contains prices for the FGBL. The column next to it calculates the effective interest rate for this price. Then, we simulate various interest rate changes – from a 6% decrease in the interest rate level (which is currently impossible) to a 6% increase in the interest rate level (which is currently not very likely either) and calculate the change in the FGBL in %.
At a current price of 140 (green colored row), an increase in the yield of German government bonds by 100 basis points (1 percentage point) would result in a price loss of the FGBL of 7.7 % – the FGBL would then stand at around 129. A lowering of the interest rate level by 1 percentage point would cause the FGBL to rise by 8.5 %. The FGBL would then stand at around 152.
Are these values accurate?
Unfortunately, we can only roughly check our calculations. Although the fictitious bond has a duration of 10 years, according to the conditions for the futures contract, federal bonds with a residual duration of at least 8.5 years and a maximum duration of 10.5 years can be delivered. In addition, these bonds must have been emitted in an issue with a volume of at least 5 billion Euros.
The “correct” result – i.e. the interest rate level implied by the FGBL – can only be calculated indirectly by analysing the yields of German government bonds on the secondary market.
The following data sets are available to us as of the current reporting date (02.01.2014):
- Stuttgart Stock Exchange: 1.71 % (8 years), 1.91 % (9 years), no value for 10 years
- Frankfurt Stock Exchange: 1.70 % (8 years), 1.92 % (9 years), 2.11 % (10 years)
- finanzen.net: 1.71 % (8 years), 1.91 % (9 years), 1.95 % (10 years)
We are considering that the fair yield of the FGBL should be somewhere between the yield of German government bonds with a remaining duration of 8 to 9 years – otherwise there would be opportunities for arbitrage.
According to our data, the mean of the 8- and 9-year yields is 1.81%. According to our model, this implies a FGBL level of 138.01 euros. This results in a deviation (of the yield) of 0.0761 % or 7.61 basis points.
However, these two values cannot be compared exactly. The yield on German government bonds is based on spot data – i.e. current prices. The implicit yield of the FGBL is based on the next futures contract, which expires at the end of March 2014.
In other words: Investors are willing to pay 138.86 Euros for a security delivered in 3 months. If, on the other hand, the security were already due today, the value of this security would be lower, otherwise arbitrage profits could be made.
We therefore discount these 138.86 Euros by the time until the delivery date of the futures (31 March 2014) with “our” calculated yield. We therefore assume the 1.81 % as a risk-free interest rate. This cash value now amounts to 138.26 euros and implies a yield of 1.79 %. The deviation is now only 2.18 basis points – so we can be satisfied with our calculation.
You can download our calculations here (xlsx, size: 30 kb).
Anzeige